Задания, решение которых заключается в преобразовании логарифмических выражений , довольно часто встречаются на ЕГЭ.
Чтобы успешно справиться с ними при минимальной затрате времени кроме основных логарифмических тождеств, необходимо знать и правильно использовать ещё некоторые формулы.
Это: a log а b = b, где а, b > 0, а ≠ 1 (Она вытекает непосредственно из определения логарифма).
log a b = log с b / log с а или log а b = 1/log b а
где а, b, с > 0; а, с ≠ 1.
log а m b n = (m/n) log |а| |b|
где а, b > 0, а ≠ 1, m, n Є R, n ≠ 0.
а log с b = b log с а
где а, b, с > 0 и а, b, с ≠ 1
Чтобы показать справедливость четвертого равенства прологарифмируем левую и правую часть по основанию а. Получим log а (а log с b) = log а (b log с а) или log с b = log с а · log а b; log с b = log с а · (log с b / log с а); log с b = log с b.
Мы доказали равенство логарифмов, значит, равны и выражения, стоящие под логарифмами. Формула 4 доказана.
Пример 1.
Вычислите 81 log 27 5 log 5 4 .
Решение.
81 = 3 4 , 27 = 3 3 .
log 27 5 = 1/3 log 3 5, log 5 4 = log 3 4 / log 3 5. Следовательно,
log 27 5 · log 5 4 = 1/3 log 3 5 · (log 3 4 / log 3 5) = 1/3 log 3 4.
Тогда 81 log 27 5 log 5 4 = (3 4) 1/3 log 3 4 = (3 log 3 4) 4/3 = (4) 4/3 = 4 3 √4.
Самостоятельно можно выполнить следующее задание.
Вычислить (8 log 2 3 + 3 1/ log 2 3) - log 0,2 5.
В качестве подсказки 0,2 = 1/5 = 5 -1 ; log 0,2 5 = -1.
Ответ: 5.
Пример 2.
Вычислите (√11) log √3 9- log 121 81 .
Решение.
Выполним замену выражений: 9 = 3 2 , √3 = 3 1/2 , log √3 9 = 4,
121 = 11 2 , 81 = 3 4 , log 121 81 = 2 log 11 3 (использовалась формула 3).
Тогда (√11) log √3 9- log 121 81 = (11 1/2) 4-2 log 11 3 = (11) 2- log 11 3 = 11 2 / (11) log 11 3 = 11 2 / (11 log 11 3) = 121/3.
Пример 3.
Вычислите log 2 24/ log 96 2- log 2 192 / log 12 2.
Решение.
Логарифмы, содержащиеся в примере, заменим логарифмами с основанием 2.
log 96 2 = 1/log 2 96 = 1/log 2 (2 5 · 3) = 1/(log 2 2 5 + log 2 3) = 1/(5 + log 2 3);
log 2 192 = log 2 (2 6 · 3) = (log 2 2 6 + log 2 3) = (6 + log 2 3);
log 2 24 = log 2 (2 3 · 3) = (log 2 2 3 + log 2 3) = (3 + log 2 3);
log 12 2 = 1/log 2 12 = 1/log 2 (2 2 · 3) = 1/(log 2 2 2 + log 2 3) = 1/(2 + log 2 3).
Тогда log 2 24 / log 96 2 – log 2 192 / log 12 2 = (3 + log 2 3) / (1/(5 + log 2 3)) – ((6 + log 2 3) / (1/(2 + log 2 3)) =
= (3 + log 2 3) · (5 + log 2 3) – (6 + log 2 3)(2 + log 2 3).
После раскрытия скобок и приведения подобных слагаемых получим число 3. (При упрощении выражения можно log 2 3 обозначить через n и упрощать выражение
(3 + n) · (5 + n) – (6 + n)(2 + n)).
Ответ: 3.
Самостоятельно можно выполнить следующее задание:
Вычислить (log 3 4 + log 4 3 + 2) · log 3 16 · log 2 144 3 .
Здесь необходимо сделать переход к логарифмам по основанию 3 и разложение на простые множители больших чисел.
Ответ:1/2
Пример 4.
Даны три числа А = 1/(log 3 0,5), В = 1/(log 0,5 3), С = log 0,5 12 – log 0,5 3. Расположите их в порядке возрастания.
Решение.
Преобразуем числа А = 1/(log 3 0,5) = log 0,5 3; С = log 0,5 12 – log 0,5 3 = log 0,5 12/3 = log 0,5 4 = -2.
Сравним их
log 0,5 3 > log 0,5 4 = -2 и log 0,5 3 < -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.
Или -2 < log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.
Ответ. Следовательно, порядок размещения чисел: С; А; В.
Пример 5.
Сколько целых чисел расположено на интервале (log 3 1 / 16 ; log 2 6 48).
Решение.
Определим между какими степенями числа 3 находится число 1 / 16 . Получим 1 / 27 < 1 / 16 < 1 / 9 .
Так как функция у = log 3 х – возрастающая, то log 3 (1 / 27) < log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.
log 6 48 = log 6 (36 · 4 / 3) = log 6 36 + log 6 (4 / 3) = 2 + log 6 (4 / 3). Сравним log 6 (4 / 3) и 1 / 5 . А для этого сравним числа 4 / 3 и 6 1/5 . Возведём оба числа в 5 степень. Получим (4 / 3) 5 = 1024 / 243 = 4 52 / 243 < 6. Следовательно,
log 6 (4 / 3) < 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.
Следовательно, интервал (log 3 1 / 16 ; log 6 48) включает в себя промежуток [-2; 4] и на нём размещаются целые числа -2; -1; 0; 1; 2; 3; 4.
Ответ: 7 целых чисел.
Пример 6.
Вычислите 3 lglg 2/ lg 3 - lg20.
Решение.
3 lg lg 2/ lg 3 = (3 1/ lg3) lg lg 2 = (3 lо g 3 10) lg lg 2 = 10 lg lg 2 = lg2.
Тогда 3 lglg2/lg3 - lg 20 = lg 2 – lg 20 = lg 0,1 = -1.
Ответ: -1.
Пример 7.
Известно, что log 2 (√3 + 1) + log 2 (√6 – 2) = А. Найдите log 2 (√3 –1) + log 2 (√6 + 2).
Решение.
Числа (√3 + 1) и (√3 – 1); (√6 – 2) и (√6 + 2) – сопряжённые.
Проведем следующее преобразование выражений
√3 – 1 = (√3 – 1) · (√3 + 1)) / (√3 + 1) = 2/(√3 + 1);
√6 + 2 = (√6 + 2) · (√6 – 2)) / (√6 – 2) = 2/(√6 – 2).
Тогда log 2 (√3 – 1) + log 2 (√6 + 2) = log 2 (2/(√3 + 1)) + log 2 (2/(√6 – 2)) =
Log 2 2 – log 2 (√3 + 1) + log 2 2 – log 2 (√6 – 2) = 1 – log 2 (√3 + 1) + 1 – log 2 (√6 – 2) =
2 – log 2 (√3 + 1) – log 2 (√6 – 2) = 2 – А.
Ответ: 2 – А.
Пример 8 .
Упростите и найдите приближенное значение выражения (log 3 2 · log 4 3 · log 5 4 · log 6 5 · … · log 10 9.
Решение.
Все логарифмы приведём к общему основанию 10.
(log 3 2 · log 4 3 · log 5 4 · log 6 5 · … · log 10 9 = (lg 2 / lg 3) · (lg 3 / lg 4)· (lg 4 / lg 5) · (lg 5 / lg 6) · … · (lg 8 / lg 9) · lg 9 = lg 2 ≈ 0,3010. (Приближенное значение lg 2 можно найти с использованием таблицы, логарифмической линейки либо калькулятора).
Ответ: 0,3010.
Пример 9 .
Вычислить log а 2 b 3 √(a 11 b -3), если log √ а b 3 = 1. (В этом примере, а 2 b 3 – основание логарифма).
Решение.
Если log √ а b 3 = 1, то 3/(0,5 log а b = 1. И log а b = 1/6.
Тогда log а 2 b 3√(a 11 b -3) = 1/2 log а 2 b 3 (a 11 b -3) = log а (a 11 b -3) / (2log а (a 2 b 3)) = (log а a 11 + log а b -3) / (2(log а a 2 + log а b 3)) = (11 – 3log а b) / (2(2 + 3log а b)) Учитывая то, что log а b = 1/6 получим (11 – 3 · 1 / 6) / (2(2 + 3 · 1 / 6)) = 10,5/5 = 2,1.
Ответ: 2,1.
Самостоятельно можно выполнить следующее задание:

Вычислить log √3 6 √2,1, если log 0,7 27 = а.
Ответ: (3 + а) / (3а).
Пример 10.
Вычислить 6,5 4/ log 3 169 · 3 1/ log 4 13 + log125.
Решение.
6,5 4/ log 3 169 · 3 1/ log 4 13 + log 125 = (13/2) 4/2 log 3 13 · 3 2/ log 2 13 + 2log 5 5 3 = (13/2) 2 log 13 3 · 3 2 log 13 2 + 6 = (13 log 13 3 / 2 log 13 3) 2 · (3 log 13 2) 2 + 6 = (3/2 log 13 3) 2 · (3 log 13 2) 2 + 6 = (3 2 /(2 log 13 3) 2) · (2 log 13 3) 2 + 6.
(2 log 13 3 = 3 log 13 2 (формула 4))
Получим 9 + 6 = 15.
Ответ: 15.
Остались вопросы? Не знаете, как найти значение логарифмического выражения?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Сейчас мы взглянем на преобразование выражений, содержащих логарифмы, с общих позиций. Здесь мы разберем не только преобразование выражений с использованием свойств логарифмов, а рассмотрим преобразование выражений с логарифмами общего вида, которые содержат не только логарифмы, но и степени, дроби, корни и т.д. Весь материал по обыкновению будем снабжать характерными примерами с детальными описаниями решений.
Навигация по странице.
Выражения с логарифмами и логарифмические выражения
Выполнение действий с дробями
В предыдущем пункте мы разобрали основные преобразования, которые проводятся с отдельными дробями, содержащими логарифмы. Эти преобразования, естественно, можно проводить с каждой отдельной дробью, являющейся частью более сложного выражения, например, представляющего собой сумму, разность, произведение и частное подобных дробей. Но помимо работы с отдельными дробями, преобразование выражений указанного вида часто подразумевает выполнение соответствующих действий с дробями. Дальше мы рассмотрим правила, по которым эти действия проводятся.
Еще с 5-6 классов нам известны правила, по которым выполняются . В статье общий взгляд на действия с дробями мы распространили эти правила с обыкновенных дробей на дроби общего вида A/B , где A и B – некоторые числовые, буквенные выражения или выражения с переменными, причем B тождественно не равно нулю. Понятно, что дроби с логарифмами являются частными случаями дробей общего вида. И в связи с этим понятно, что действия с дробями, которые содержат в своих записях логарифмы, проводятся по тем же правилам. А именно:
- Чтобы сложить или вычесть две дроби с одинаковыми знаменателями, надо соответственно сложить или вычесть числители, а знаменатель оставить прежним.
- Чтобы сложить или вычесть две дроби с разными знаменателями, надо привести их к общему знаменателю и выполнить соответствующие действия по предыдущему правилу.
- Чтобы умножить две дроби, надо записать дробь, числителем которой является произведение числителей исходных дробей, а знаменателем – произведение знаменателей.
- Чтобы разделить дробь на дробь, надо делимую дробь умножить на дробь, обратную делителю, то есть, на дробь, с переставленными местами числителем и знаменателем.
Приведем несколько примеров на выполнение действий с дробями, содержащими логарифмы.
Пример.
Выполните действия с дробями, содержащими логарифмы: а) , б)  , в)
, в)  , г)
, г)  .
.
Решение.
а) Знаменатели складываемых дробей, очевидно, одинаковые. Поэтому, согласно правилу сложения дробей с одинаковыми знаменателями складываем числители, а знаменатель оставляем прежним: ![]() .
.
б) Здесь знаменатели различные. Поэтому, сначала нужно привести дроби к одинаковому знаменателю
. В нашем случае знаменатели уже представлены в виде произведений, и нам остается взять знаменатель первой дроби и добавить к нему недостающие множители из знаменателя второй дроби. Так мы получим общий знаменатель вида ![]() . При этом к общему знаменателю вычитаемые дроби приводятся при помощи дополнительных множителей в виде логарифма и выражения x 2 ·(x+1)
соответственно. После этого останется выполнить вычитание дробей с одинаковыми знаменателями, что не представляет сложностей.
. При этом к общему знаменателю вычитаемые дроби приводятся при помощи дополнительных множителей в виде логарифма и выражения x 2 ·(x+1)
соответственно. После этого останется выполнить вычитание дробей с одинаковыми знаменателями, что не представляет сложностей.
Итак, решение таково:
в) Известно, что результатом умножения дробей является дробь, числитель которой есть произведение числителей, а знаменатель – произведение знаменателей, поэтому
Несложно заметить, что можно провести сокращение дроби
на двойку и на десятичный логарифм, в результате имеем  .
.
г) Переходим от деления дробей к умножению, заменяя дробь-делитель обратной ей дробью . Так
Числитель полученной дроби можно представить в виде ![]() , из которого явно виден общий множитель числителя и знаменателя – множитель x
, на него можно сократить дробь:
, из которого явно виден общий множитель числителя и знаменателя – множитель x
, на него можно сократить дробь:
Ответ:
а) , б)  , в)
, в)  , г)
, г)  .
.
Следует помнить, что действия с дробями проводятся с учетом порядка выполнения действий : сначала умножение и деление, затем сложение и вычитание, а если есть скобки, то сначала проводятся действия в скобках.
Пример.
Выполните действия с дробями  .
.
Решение.
Сначала выполняем сложение дробей в скобках, после чего будем проводить умножение:
Ответ:
В этом пункте остается проговорить вслух три довольно очевидных, но в то же время важных момента:
Преобразование выражений с использованием свойств логарифмов
Наиболее часто преобразование выражений с логарифмами подразумевает использование тождеств, выражающих определение логарифма и
ЕГОРОВА ВИКТОРИЯ ВАЛЕРЬЕВНА
Учитель математики
высшей квалификационной категории
ТЕМА: «ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ
ЛОГАРИФМИЧЕСКИХ ВЫРАЖЕНИЙ»
Знания и навыки, которыми должны овладеть учащиеся после изучения данного урока:
знать определение логарифма числа, основное логарифмическое тождество, свойства логарифмов;
уметь выполнять преобразования выражений, содержащих логарифмы, вычислять логарифмы.
Литература:
1. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений. – М.: Просвещение, 2001.
2. Кочагин В.В., Кочагина М.В., Интенсивный курс подготовки к ЕГЭ. – М.:Эксмо, 2009.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Алгебраический тренажер: Пособие для школьников и абитуриентов. – М.:Илекса, 2005.
4. Гусев В.А., Мордкович А.Г. Математика: Справочные материалы: Книга для учащихся. – М.: Просвещение, 2001.
План урока:
Ход урока:
1) Логарифм – это греческое слово, которое состоит из 2-х слов: “логос”- отношение, “аритмос”- число. Значит, логарифм есть число, измеряющее отношение. В публикации тысяча шестьсот четырнадцатого года сообщалось, что Непер изобрёл логарифмы. Позже им были составлены логарифмические таблицы, которые теперь известны нам как таблицы Брадиса. Менее чем за одно столетие таблицы распространились по всему миру и сделались незаменимым вычислительным средством. В дальнейшем они были, как бы встроены в удобное устройство, чрезвычайно ускоряющее процесс вычисления – логарифмическую линейку, которой пользовались до семидесятых годов двадцатого века.
Приложение 1.
2) Логарифмом положительного числа b по основанию a , причём а больше нуля и не равно единицы, называется показатель степени, в которую нужно возвести число a , чтобы получить число b.
Это равенство, выражающее определение логарифма, называется основным логарифмическим тождеством .
Ц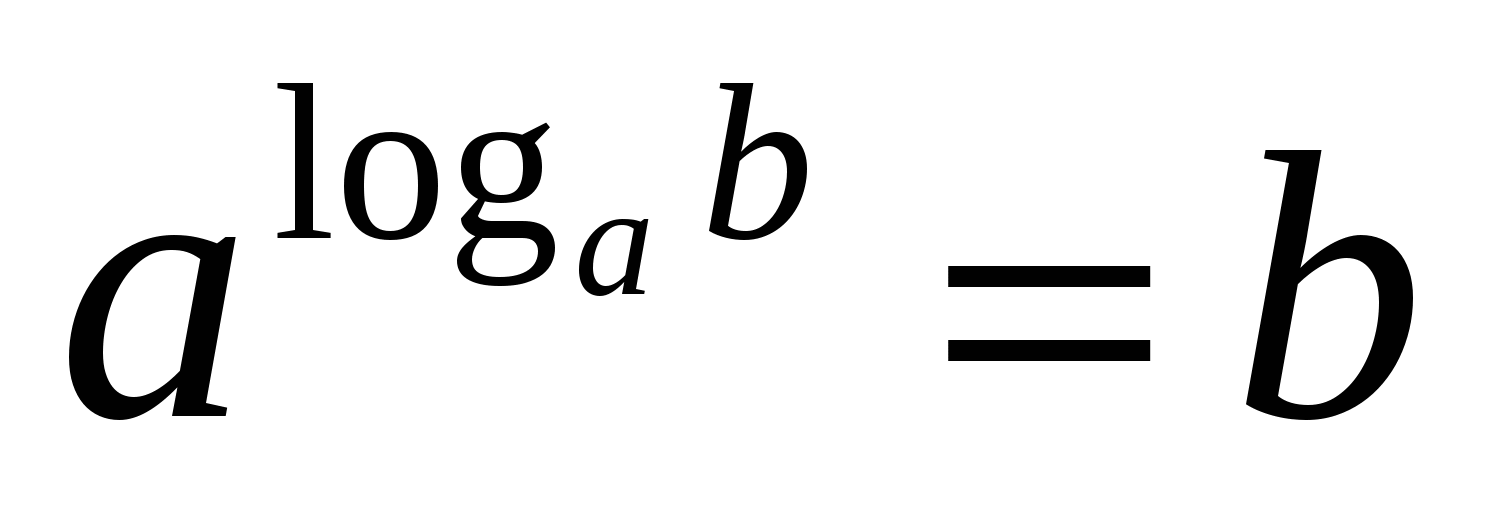
ОР 1
П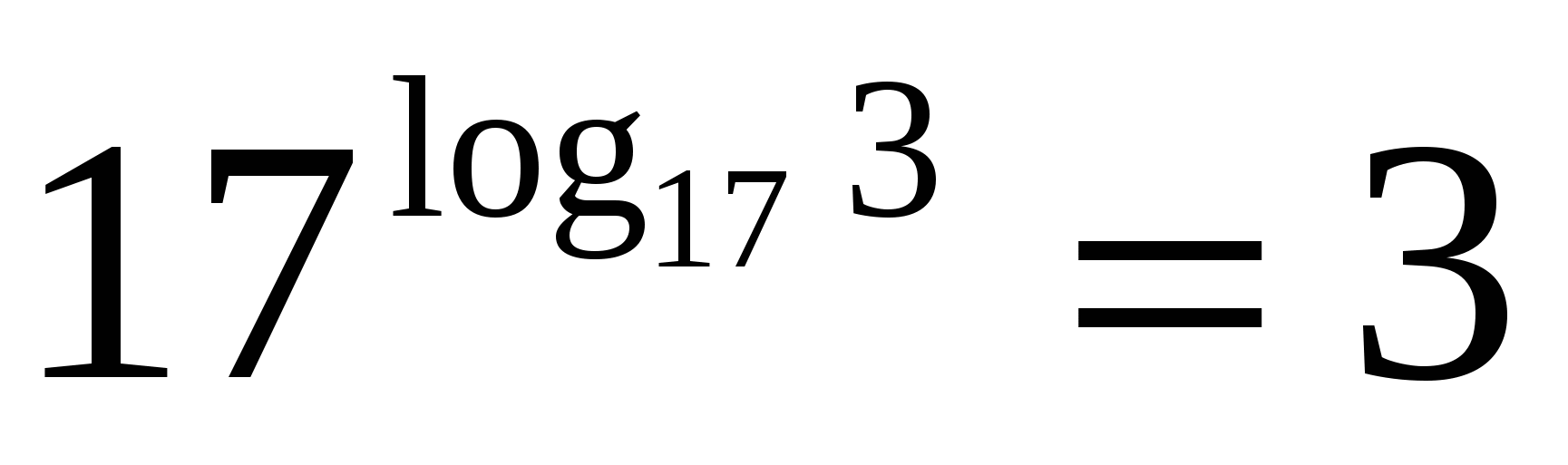
Основание степени и основание логарифма семнадцать, значит по основному логарифмическому тождеству значение выражения равно трём.
Оработаем устно:
Щ ЕЛЧОК
ЕЛЧОК

Одна вторая равна нуль целых пяти десятым, значит выражение равно арифметическому квадратному корню из пяти.
П
 риложение 2.
риложение 2.
Равенство означает, что
Из определения логарифма получаются следующие важные равенства:
Например:

П риложение 3.
риложение 3.
Перейдем к заданиям ЕГЭ:
Приложение 4.
3 )
Для логарифма по основанию десять существует специальное обозначение и название
десятичный логарифм
.
)
Для логарифма по основанию десять существует специальное обозначение и название
десятичный логарифм
.
Л огарифм по основанию
е
называется
натуральным логарифмом
.
огарифм по основанию
е
называется
натуральным логарифмом
.
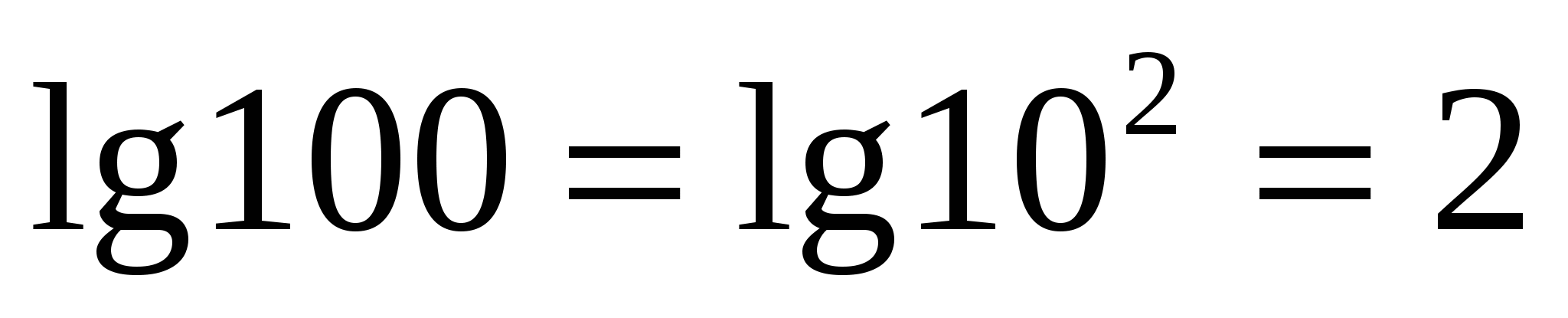
Н апример,
апример,

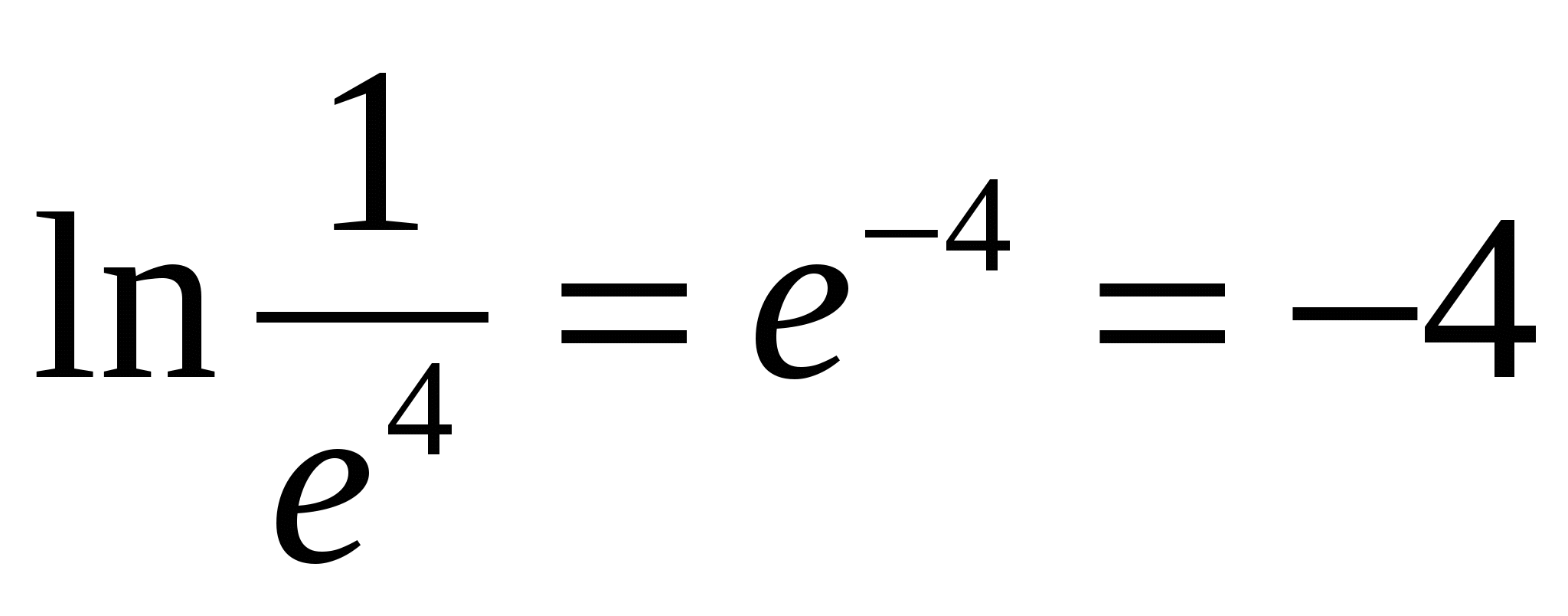
4) Из определения логарифма вытекают следующие его свойства. Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов.
Логарифм произведения двух положительных чисел по основанию а равен сумме логарифмов этих чисел с тем же основанием.
ЦОР 2
Например,
З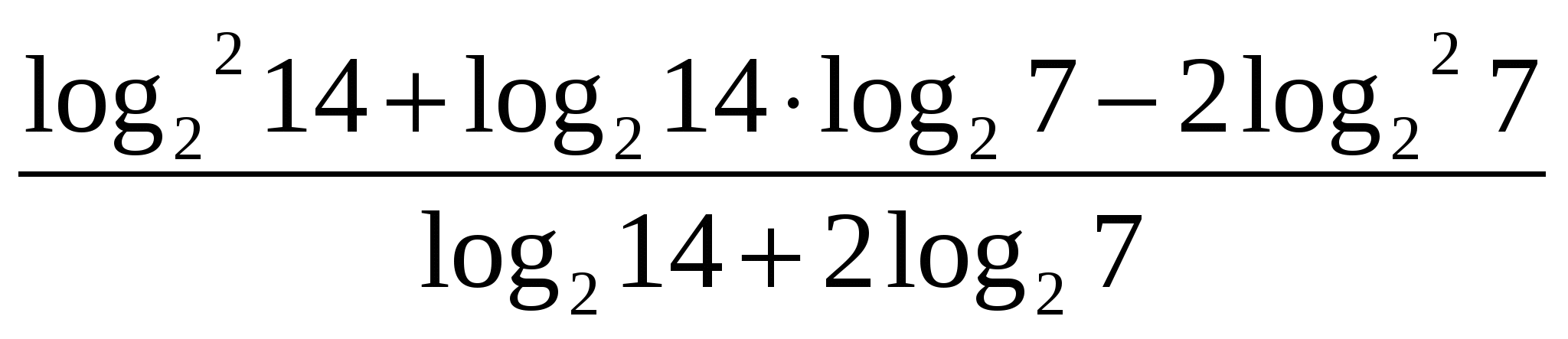 адание 1.
адание 1.
Задание 2. Упростите выражение
В оспользуемся решением предыдущего примера. Заменим
оспользуемся решением предыдущего примера. Заменим
Обратите внимание на то, что логарифм в квадрате, поэтому и сумму необходимо возвести в квадрат. Применяя формулу квадрата суммы, раскроем скобки. Приведём подобные слагаемые.
5) Логарифм частного равен разности логарифмов делимого и делителя.
Ц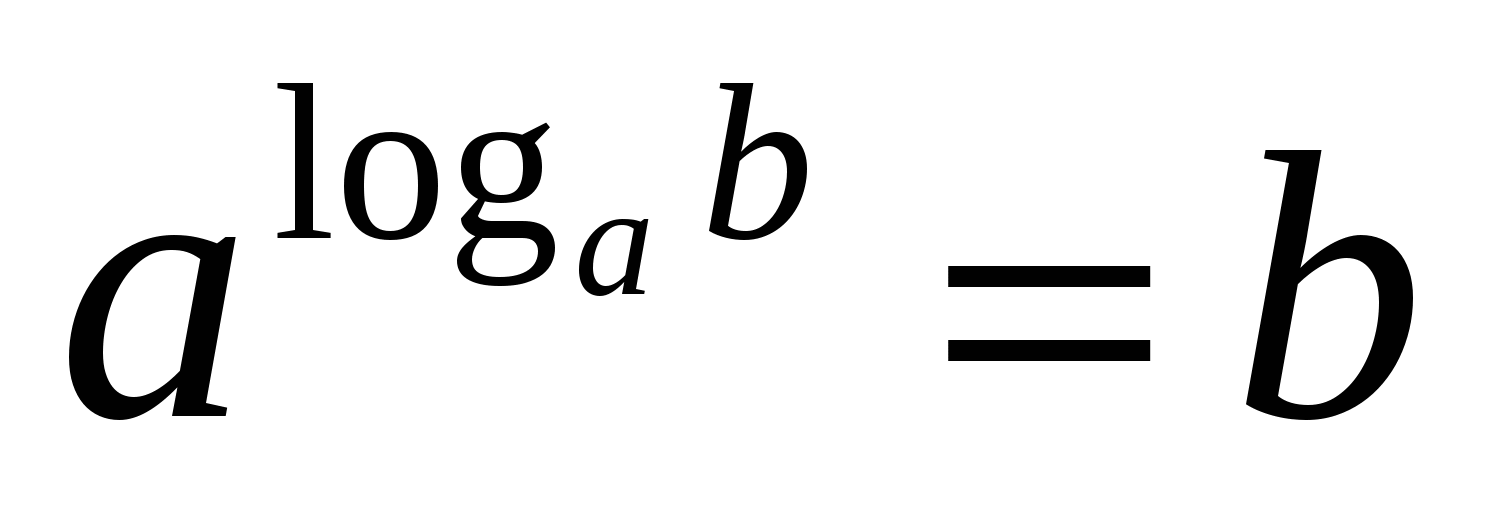
Обратите внимание на основание степени и основание логарифма – они одинаковы.
ОР 3Р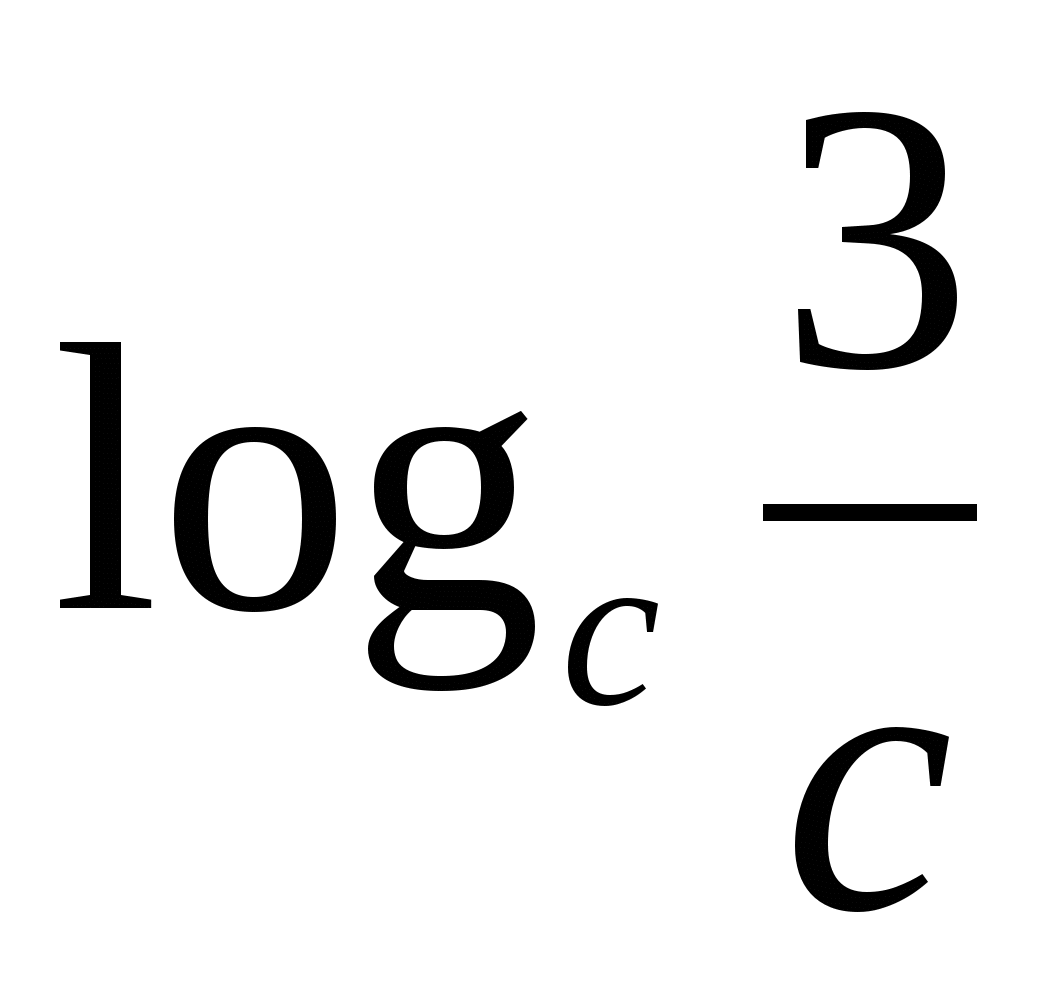
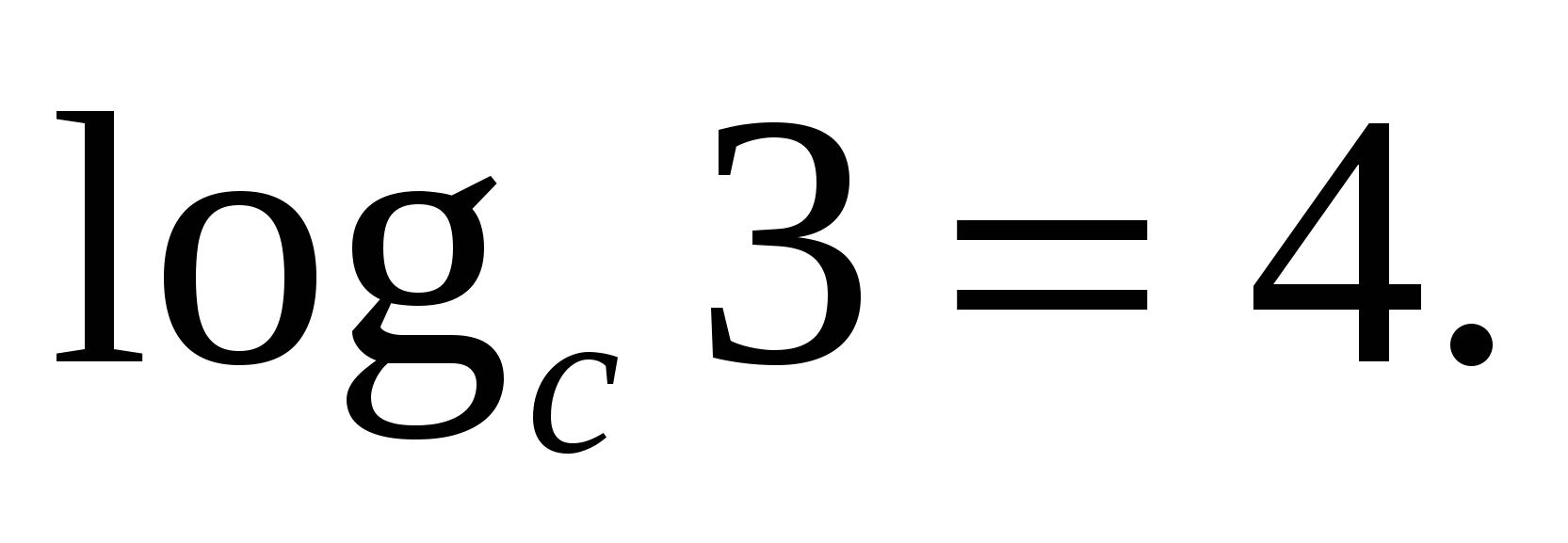 ассмотрим применение этой формулы на примере:
ассмотрим применение этой формулы на примере:
З адание 1.
Найдите значение выражения, если
адание 1.
Найдите значение выражения, если

Задание 2. Найдите значение b по его логарифму
6) Логарифм степени по основанию а , равен произведению показателя степени на логарифм по тому же основанию.
ЦОР 4
Например,


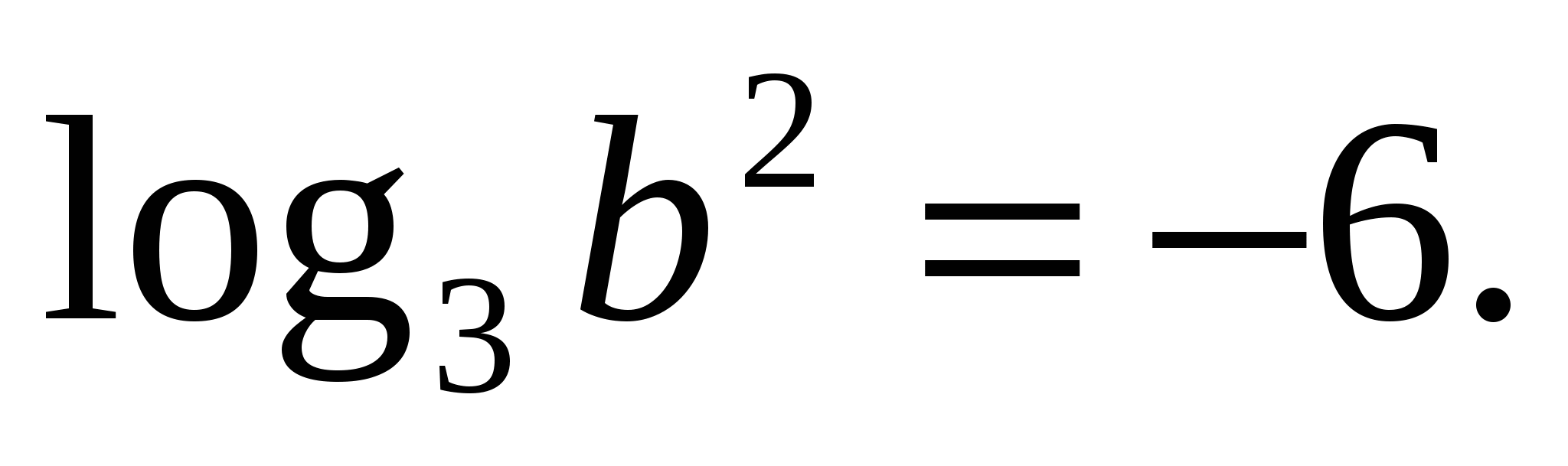
З адание 1.
Вычислите, если
адание 1.
Вычислите, если
Упростим выражение
Формула
называется формулой перехода к новому основанию.
З
 адание 1.
Выразить через логарифм с основанием 2.
адание 1.
Выразить через логарифм с основанием 2.
Задание 2. Вычислите
ЦОР 5
 ЦОР 6
ЦОР 6
Например,
З
 адание 1.
Вычислите
адание 1.
Вычислите

З адание 2.
Вычислите
адание 2.
Вычислите
9) К логарифмическим преобразованиям можно приступать, только в том случаи, если вы запомнили все свойства логарифмов. Повторив их, рассмотрим задания на преобразования логарифмических выражений с другой стороны.
Для преобразования суммы или разности логарифмических выражений иногда достаточно использовать определение логарифма, а чаще всего свойства логарифма произведения или частного.
З адание 1.
Вычислите
адание 1.
Вычислите
Решим двумя способами.
1 способ, используя определение логарифма:
2 способ, опираясь на свойство логарифма частного:

Задание 2. Найдите значение выражения
Применим сначала формулу логарифма произведения, затем определение логарифма.
Основное логарифмическое тождество используется при преобразовании выражений, содержащих логарифм в показателе степени. Идея таких операций заключается в получении равных основания степени и основания логарифма.
Иногда необходимо преобразовывать выражение по свойствам логарифма и по свойствам степени, так же можно легко перейти от одного основания к другому, используя формулу перехода. В других случаях следует применять несколько свойств.
З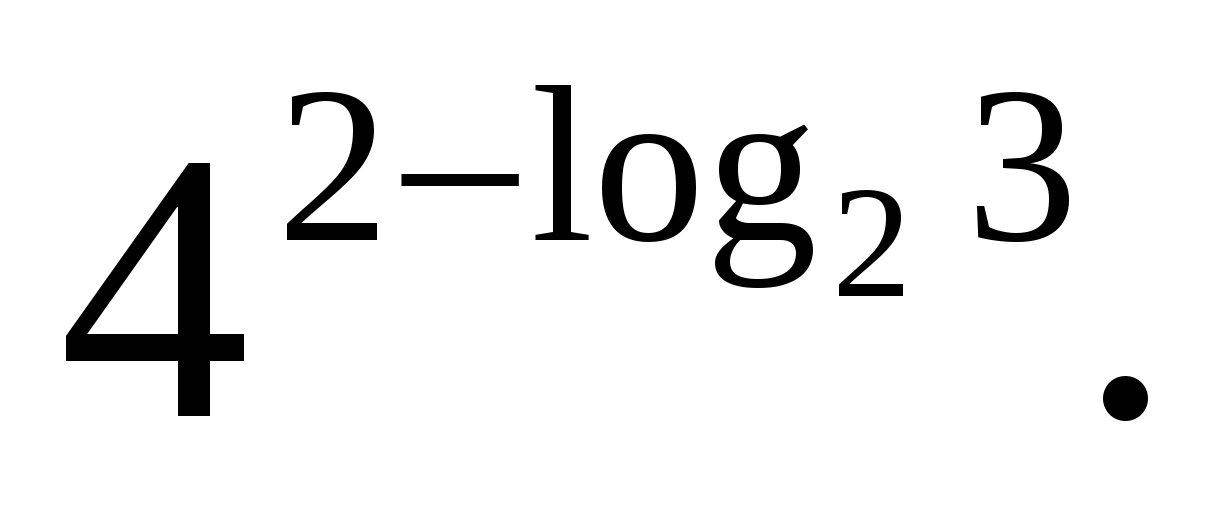 адание 3.
Вычислите
адание 3.
Вычислите
З адание 4.
Найдите значение выражения
адание 4.
Найдите значение выражения
Задание 5. Найдите значение выражения
З адание 6.
Представьте в виде разности логарифмов
адание 6.
Представьте в виде разности логарифмов
Н аибольшую трудность представляют преобразования логарифмических выражений, находящихся под радикалом. В процессе преобразований приходится рассматривать модули логарифмических выражений, для раскрытия которых требуется сравнить иррациональные числа или рациональное и иррациональное число. Будем действовать последовательно. Рассмотрим выражение, стоящее под внутренним радикалом.
аибольшую трудность представляют преобразования логарифмических выражений, находящихся под радикалом. В процессе преобразований приходится рассматривать модули логарифмических выражений, для раскрытия которых требуется сравнить иррациональные числа или рациональное и иррациональное число. Будем действовать последовательно. Рассмотрим выражение, стоящее под внутренним радикалом.
Подставим в исходное выражение.
 Следует отметить, что с преобразованием логарифмических выражений можно встретиться и при решении уравнений и неравенств или исследовании функций, поэтому в неявном виде они могут присутствовать и в заданиях групп В и С.
Следует отметить, что с преобразованием логарифмических выражений можно встретиться и при решении уравнений и неравенств или исследовании функций, поэтому в неявном виде они могут присутствовать и в заданиях групп В и С.
10) Подведение итогов.Вопросы:
Логарифм по основанию 10 называется
основным логарифмом
главным логарифмом
натуральным логарифмом
десятичным логарифмом
2) Какие значения может принимать
x
в выражении 
Значение не определено
5) Укажите соотношение, которое верно для всех x ≠ 0 .
6) Укажите верное соотношение для формулы перехода к новому основанию.
7) Укажите верное равенство при

Математика. Тематические тесты. Часть II. Подготовка к ЕГЭ-2010. 10-11 классы. Под ред. Лысенко Ф.Ф. - Ростов н/Д.: Легион, 2009. - 176с.
Математика. ЕГЭ-2009. Тематические тесты. Ч.II (В4-В8, С1-С2) Под ред. Лысенко Ф.Ф. - Ростов н/ Д: Легион, 2008 - 160 с.
Пособие состоит из тестов по отдельным темам, которые являются традиционными в курсе математики и потому, как правило, входят в ЕГЭ. Они полностью охватывают группы заданий повышенного и высокого уровня сложности ЕГЭ, кроме текстовых задач и задач по геометрии. По каждой теме предлагается один или более комплектов тестов. В каждом комплекте по 10 тестов, в каждом тесте содержится 8 заданий.
Цель настоящей книги - отработать задания с кратким
и развернутым ответом тестов ЕГЭ. Она необходима в первую очередь выпускникам,
рассчитывающим получить на ЕГЭ хорошую оценку, а также учащимся 10-х классов,
которые могут закрепить пройденные темы под углом зрения ЕГЭ. Предлагаемое
пособие может быть полезно всем выпускникам, готовящимся к ЕГЭ по математике, а
также педагогам, осуществляющим подготовку учащихся к ЕГЭ.
Формат: djvu / zip (2009 , 176с.)
Размер: 2,5 Мб
Скачать / Download файл 14
Формат: pdf (2009 , 176с.)
Размер: 8 ,6 Мб
Скачать: 14 .12.2018г, ссылки удалены по требованию изд-ва "Легион" (см. примечание)
Формат: djvu / zip (2008 , 160с.)
Размер: 3 Мб
Скачать / Download файл 14 .12.2018г, ссылки удалены по требованию изд-ва "Легион" (см. примечание)
Формат: pdf (2008 , 160с.)
Размер: 9 ,9 Мб
Скачать: 14 .12.2018г, ссылки удалены по требованию изд-ва "Легион" (см. примечание)
Учебно-методический комплекс
"Математика. ЕГЭ-2010" под ред. Лысенко Ф.Ф. и Кулабухова С.Ю. включает
учебные пособия:
1.
Математика. Подготовка к ЕГЭ-2010.
2. Решебник. Математика. Подготовка к ЕГЭ-2010.
3. Математика. Тематические тесты. Часть I (базовый
уровень). Подготовка к ЕГЭ-2010. 10-11 классы.
4. Математика. Тематические тесты. Часть II.
Подготовка к ЕГЭ-2010. 10-11 классы.
5.
Математика. Тематические тесты: геометрия, текстовые задачи.
Подготовка к ЕГЭ-2010. 10-11 классы.
6.
Математика. Сборник тестов ЕГЭ 2001 - 2010.
7. Математика. Подготовка к ЕГЭ-2010.
Учебно-тренировочные тесты.
8. Карманный справочник по математике.
Оглавление
От авторов 11
§ 1. Тождественные
преобразования логарифмических выражений 13
Вариант №1 13
Вариант №2 13
Вариант №3 14
Вариант №4 14
Вариант №5 15
Вариант №6 15
Вариант №7 16
Вариант №8 16
Вариант №9 17
Вариант №10 17
§ 2. Тождественные
преобразования выражений, содержащих степень 18
Вариант №1 18
Вариант №2 19
Вариант №3 19
Вариант №4 20
Вариант №5 21
Вариант №6 21
Вариант №7 22
Вариант №8 23
Вариант №9 23
Вариант №10 24
§ 3. Тождественные
преобразования иррациональных выражений 25
Вариант №1 25
Вариант №2 25
Вариант №3 26
Вариант №4 26
Вариант №5 27
Вариант №6 28
Вариант №7 28
Вариант №8 29
Вариант №9 30
Вариант №10 30
§ 4. Системы уравнений 31
Вариант №1 31
Вариант №2 32
Вариант №3 33
Вариант №4 33
Вариант №5 34
Вариант №6 35
Вариант №7 36
Вариант №8 37
Вариант №9 38
Вариант №10 39
§ 5. Геометрический смысл
производной 39
Вариант №1 39
Вариант №2 41
Вариант №3 43
Вариант №4 44
Вариант №5 46
Вариант №6 48
Вариант №7 50
Вариант №8 52
Вариант №9 54
Вариант №10 55
§ 6. Неравенства 56
Вариант №1 г 56
Вариант №2 57
Вариант №3 58
Вариант №4 58
Вариант №5 59
Вариант №6 60
Вариант №7 60
Вариант №8 61
Вариант №9 62
Вариант №10 63
§ 7. Иррациональные
уравнения 63
Вариант №1 63
Вариант №2 64
Вариант №3 65
Вариант №4 65
Вариант №5 66
Вариант №6 66
Вариант №7 67
Вариант №8 67
Вариант №9 68
Вариант №Ю 68
§ 8. Тригонометрические
уравнения 69
Вариант №1 69
Вариант №2 69
Вариант №3 70
Вариант №4 70
Вариант №5 71
Вариант №6 72
Вариант №7 72
Вариант №8 73
Вариант №9 74
Вариант №10 74
§ 9. Логарифмические
уравнения 75
Вариант №1 75
Вариант №2 75
Вариант №3 76
Вариант №4 76
Вариант №5 77
Вариант №6 77
Вариант №7 78
Вариант №8 * 78
Вариант №9 79
Вариант №10 79
§ 10. Показательные
уравнения 80
Вариант №1 80
Вариант №2 80
Вариант №3 81
Вариант №4 81
Вариант №5 82
Вариант №6 82
Вариант №7 83
Вариант №8 83
Вариант №9 84
Вариант №10 84
§11. Периодичность, чётность
и нечётность функций 85
Вариант №1 85
Вариант №2 86
Вариант №3 87
Вариант №4 89
Вариант №5 90
Вариант №6 91
Вариант №7 92
Вариант №8 93
Вариант №9 94
Вариант №10 95
§ 12. Нули сложной функции.
Ограниченность функции 97
Вариант №1 97
Вариант №2 97
Вариант №3 98
Вариант №4 98
Вариант №5 99
Вариант №6 99
Вариант №7 100
Вариант №8 100
Вариант №9 101
Вариант №10 101
§ 13. Область определения,
множество значений, монотонность функций 102
Вариант №1 102
Вариант №2 102
Вариант №3 103
Вариант №4 103
Вариант №5 104
Вариант №6 104
Вариант №7 105
Вариант №8 105
Вариант №9 106
Вариант №10 107
§ 14. Экстремумы функции.
Наибольшее и наименьшее значения функции 107
Вариант №1 107
Вариант №2 108
Вариант №3 108
Вариант №4 109
Вариант №5 109
Вариант №6 110
Вариант №7 110
Вариант №8 111
Вариант №9 111
Вариант №10 112
§ 15. Различные приёмы при
решении логарифмических уравнений 113
Вариант №1 113
Вариант №2 113
Вариант №3 114
Вариант №4 114
Вариант №5 115
Вариант №6 115
Вариант №7 116
Вариант №8 116
Вариант №9 117
Вариант №10 117
§ 16. Различные приёмы при
решении тригонометрических уравнений 118
Вариант №1 118
Вариант №2 118
Вариант №3 118
Вариант №4 119
Вариант №5 119
Вариант №6 120
Вариант №7 120
Вариант №8 121
Вариант №9 121
Вариант №10 122
§ 17. Различные приёмы при
решении иррациональных уравнений 123
Вариант №1 123
Вариант №2 123
Вариант №3 124
Вариант №4 124
Вариант №5 125
Вариант №6 125
Вариант №7 125
Вариант №8 126
Вариант №9 126
Вариант № 10 127
§ 18. Уравнения, содержащие
переменную под знаком модуля 127
Вариант №1 127
Вариант №2 128
Вариант №3 128
Вариант №4 129
Вариант №5 129
Вариант №6 130
Вариант №7 130
Вариант №8 131
Вариант №9 131
Вариант №10 131
§ 19. Различные приёмы при
решении показательных уравнений.132
Вариант №1 132
Вариант №2 133
Вариант №3 133
Вариант №4 134
Вариант №5 134
Вариант №6 135
Вариант №7 135
Вариант №8 135
Вариант №9 136
Вариант №10 136
§ 20. Различные приёмы при
решении комбинированных уравнений 137
Вариант №1 137
Вариант №2 137
Вариант №3 138
Вариант №4 138
Вариант №5 139
Вариант №6 139
Вариант №7 140
Вариант №8 140
Вариант №9 141
Вариант №10 141
§ 21. Уравнения с
параметром, содержащие модуль 142
Вариант №1 142
Вариант №2 142
Вариант №3 143
Вариант №4 144
Вариант №5 144
Вариант №6 145
Вариант №7 146
Вариант №8 146
Вариант №9 147
Вариант №10 148
Ответы 149
§ 1. Тождественные преобразования логарифмических выражений 149
§ 2. Тождественные преобразования выражений, содержащих степень 150
§ 3. Тождественные преобразования иррациональных выражений 150
§ 4. Системы уравнений 151
§ 5. Геометрический смысл производной 151
§ 6. Неравенства 152
§ 7. Иррациональные уравнения 152
§ 8. Тригонометрические уравнения 153
§ 9. Логарифмические уравнения 153
§ 10. Показательные уравнения 154
§11. Периодичность, четность и нечетность функций 154
§ 12. Нули сложной функции. Ограниченность функции 155
§ 13. Область определения, множество значений, монотонность функций 156
§ 14. Экстремумы функции. Наибольшее и наименьшее значения функции 158
§ 15. Различные приемы при решении логарифмических уравнений 159
§ 16. Различные приемы при решении тригонометрических уравнений 160
§ 17. Различные приемы при решении иррациональных уравнений 164
§ 18. Уравнения, содержащие переменную под знаком модуля 165
§ 19. Различные приемы при решении показательных уравнений.166
§ 20. Различные приемы при решении комбинированных уравнений 167
§ 21. Уравнения с параметром, содержащие модуль 169
Литература 170







